In this article, I will briefly explore Stacks and Queues. We will also look at how we can implement these data structures in Swift, and furthermore, we’ll look at the types of applications for which we can use stacks and queues.
As an aside, you will often hear stacks referenced in the context of memory management. This isn’t the topic of this article, but you can find out all about
Stacks vs Heaps in the context of memory management here,
or about memory management in Xcode with ARC here.
The Stack Data Structure
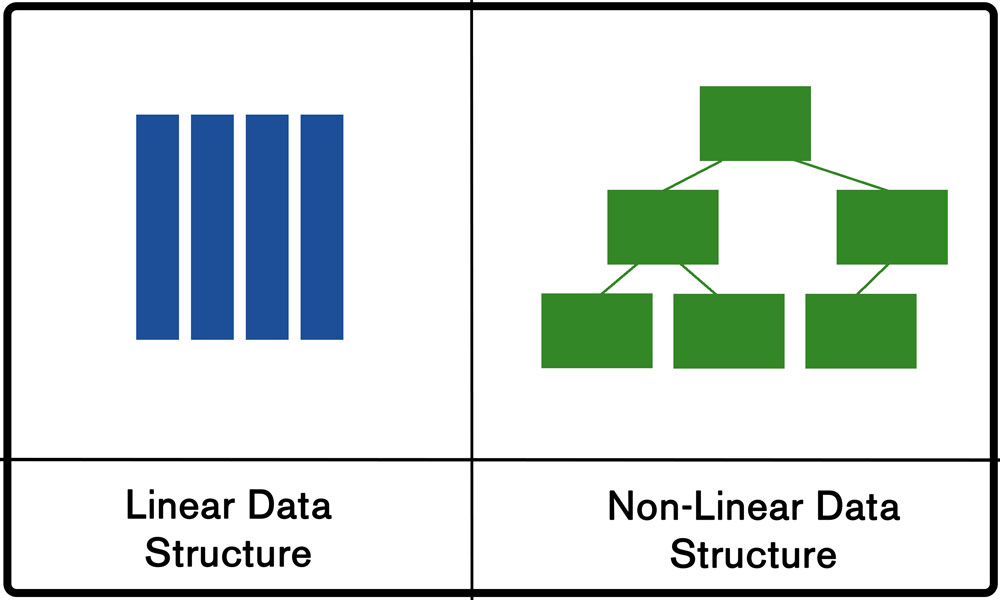
The Stack is a Linear Data Structure, and it follows a particular order in which operations can be performed. As such, a Stack arranges data into a sequence and also has the characteristic of following a defined order in which operations may be performed (Ref#: B). In contrast, a non-linear data structure doesn’t organize its data in a strictly sequential manner (for example, Trees and Graphs are non-linear) (Ref#: G).
Typically, when we talk about a “stack,” we’re referring to a structure that gives you LIFO (last-in-first-out) ordering. This means that the last element you add is the first element you could subsequently remove from the stack.

As noted above, a stack typically uses LIFO ordering, meaning that—like a stack of dinner plates—the most recent item (or plate) added is also the first to be removed.
Stack Operations
- Pop: The
pop()operation removes the top item from a stack. (“The items are popped in the reverse order in which they are pushed. If the stack is empty, then it is said to be an Underflow condition.”) - Push: The
push(item)operation adds an item to the top of a stack. If this is performed when the stack is full, it is referred to as an Overflow condition. - Peek (or Top): The
peek()operation returns the top element of the stack. Because of the design of a stack, we can’t arbitrarily check its contents—other than its topmost element. It’s as if we’re looking down on a stack of books; we can only see which book is on top. - isEmpty: The
isEmpty()operation returns true if and only if the stack is empty; otherwise, it returns false.
Because of how a stack is structured, unlike an array, it does not provide constant-time access to the ith item. However, adding and removing items can be done in constant time.
Applications of Stacks
A common use case for stacks is in recursive algorithms. This includes cases where your code goes through a set of operations, encounters a point of failure, and must backtrack. Stacks are also used to implement recursive algorithms iteratively (Ref#: A). Examples include the redo and undo features in photo editing software or the ability to go backward and forward in a web browser.
Other applications of stacks include:
- Balancing of symbols (e.g., when parsing code for matching opening and closing braces). “They are used to check if a given expression has balanced symbols or not. The algorithm is very useful in compilers.” Specifically, each time a parser reads one character, if the character is an opening delimiter like ‘(’, ‘{’, or ‘[’, then it is PUSHED onto the stack. When a closing delimiter such as ‘)’, ‘}’, or ‘]’ is encountered, the stack is popped. The opening and closing delimiters are compared, and if they match, parsing continues. If not, the parser indicates an error on that line (Ref#: J).
- Infix to Postfix/Prefix conversion
- Algorithms like Tower of Hanoi (see image below), Tree Traversals, Stock Span problem, and Histogram problems
- Backtracking scenarios: the Knight’s Tour problem, the rat-in-a-maze scenario, the N Queen problem, and making a sudoku solver.

In addition, we can use Stacks in Graph Algorithms like Topological Sorting and Strongly Connected Components.
Implementation
There are essentially two ways to implement a stack in code: using an array or using a linked list.
Swift Implementation Using an Array
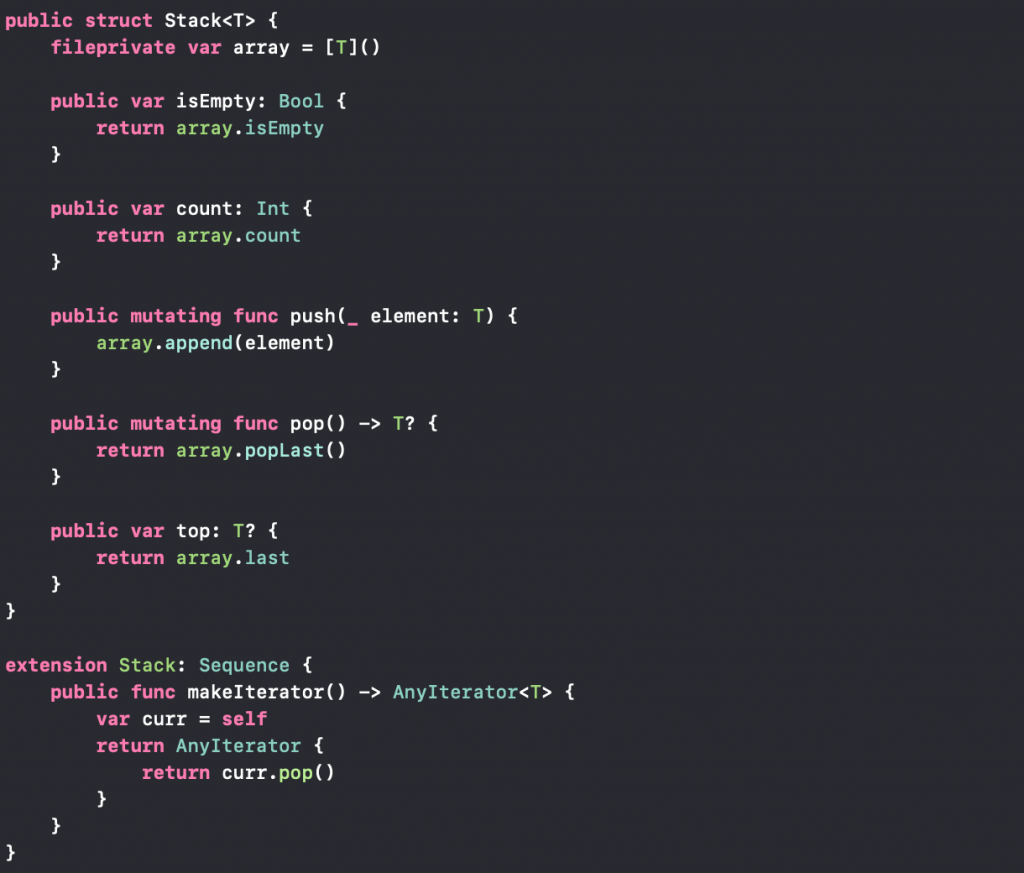
Source: Swift Algorithm Club
Swift Implementation Using a Linked List
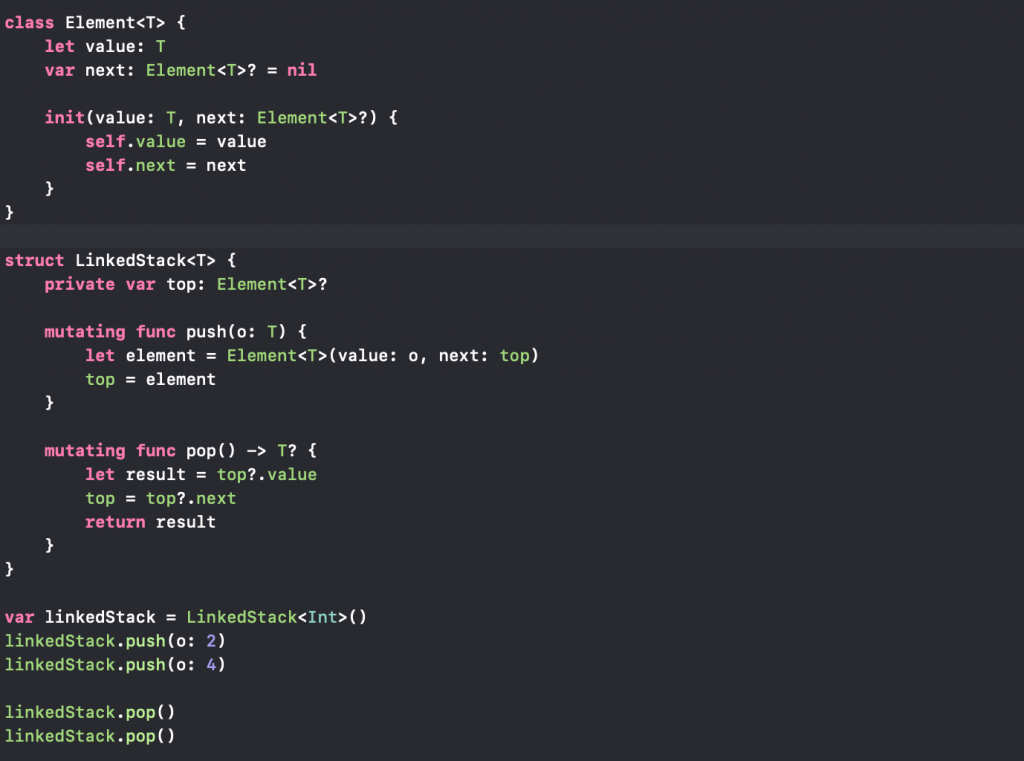
Source: Linked List Implementation Gist
The linked list implementation here is very simple, where each Element simply has an optional reference to another Element.
Queues
In contrast to a Stack, a Queue uses FIFO (first-in-first-out) ordering, which means insertions and deletions happen at different ends of the queue. In other words, “the first item you enqueue is also the first item you dequeue” (Ref#: I).

Queue Operations
- Add:
add(item)adds an item to the end of a list. This is also calledenqueue(element). - Remove:
remove()removes the first item from a list. This is also referred to asdequeue(). - Peek:
peek()returns the item at the front of the queue. - isEmpty:
isEmpty()returns true if the queue is empty; otherwise, it returns false.
Queue in Swift
Implementation Using an Array
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
// QUEUE public struct Queue { fileprivate var array = [T]() public var isEmpty: Bool { return array.isEmpty } public var count: Int { return array.count } public mutating func enqueue(_ element: T) { array.append(element) } public mutating func dequeue() -> T? { if isEmpty { return nil } else { return array.removeFirst() } } public var front: T? { return array.first } } |
Source: Swift Algorithm Club
From the above, note that we add new elements at the end and dequeue older elements from the front. As we’re using generics, we can create a queue of many different types (e.g., Int, String, etc.).
Applications of Queues
In the context of iOS development, Grand Central Dispatch (GCD) uses queues. These aren’t always simple FIFO queues, but in the case of a serial dispatch queue, operations are executed in the order in which they were added.
Beyond that, we can use queues for any scenario requiring first-in-first-out behavior. This is often useful for managing asynchronous tasks; for example, we could queue up a series of downloads and only start them when connected to Wi-Fi.
Conclusion
We have briefly covered what stacks are, how we use them, what queues are, and how we use them. Although their definitions are straightforward, they can help us solve a broad range of interesting problems.
References
A) McDowell, G.L. (2016). Cracking the Coding Interview. CareerCup, Palo Alto, CA.
B) https://www.geeksforgeeks.org/stack-data-structure/
C) https://www.geeksforgeeks.org/stack-data-structure-introduction-program/
D) https://www.raywenderlich.com/800-swift-algorithm-club-swift-stack-data-structure/
E) https://github.com/raywenderlich/swift-algorithm-club/tree/master/Stack
F) https://medium.com/devslopes-blog/swift-data-structures-stack-4f301e4fa0dc
G) https://techdifferences.com/difference-between-linear-and-non-linear-data-structure.html
H) https://www.geeksforgeeks.org/implement-a-stack-using-singly-linked-list/
I) https://github.com/raywenderlich/swift-algorithm-club/tree/master/Queue
J) http://www.studyalgorithms.com/misc/how-can-stacks-be-used-for-checking-balancing-of-symbols/
K) https://www.geeksforgeeks.org/postfix-prefix-conversion/
L) https://en.wikibooks.org/wiki/Data_Structures/Stacks_and_Queues/
![]()
Comments